
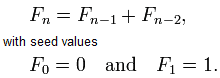
Fibonacci sequence formula golden ratio full#
The DNA molecule measures 34 angstroms long by 21 angstroms wide for each full cycle of its double helix spiral. DNA moleculesĮven the microscopic realm is not immune to Fibonacci. When a hawk approaches its prey, its sharpest view is at an angle to their direction of flight - an angle that's the same as the spiral's pitch. And as noted, bee physiology also follows along the Golden Curve rather nicely. Following the same pattern, females have 2, 3, 5, 8, 13, and so on. This formula can be used to calculate the nth Fibonacci number. We derive the celebrated Binets formula, which gives an explicit formula for the Fibonacci numbers in terms of powers of the golden ratio and its reciprocal. The ratio is derived from an ancient Indian mathematical formula which Western society named. We learn about the Fibonacci numbers, the golden ratio, and their relationship. Thus, when it comes to the family tree, males have 2, 3, 5, and 8 grandparents, great-grandparents, gr-gr-grandparents, and gr-gr-gr-grandparents respectively. The golden ratio is an irrational number that is equal to (1+5)/2, or approximately 1.618. Males have one parent (a female), whereas females have two (a female and male).

In addition, the family tree of honey bees also follows the familiar pattern. The answer is typically something very close to 1.618. The most profound example is by dividing the number of females in a colony by the number of males (females always outnumber males). It has a very interesting relationship to the Fibonacci sequence. Selecting a region changes the language and/or content on of honey bees, they follow Fibonacci in other interesting ways. The golden ratio is the number 1.618034 given by the solution to the equation x2 x + 1. Use the golden ratio as a guideline for your work to make sure things are nicely spaced out and well composed. If you just center every image or arrange text as a single unjustified block, you risk alienating your reader, viewer, or user. “If everything is important, then nothing is important,” says human factors engineering student Sara Berndt. Ultimately, spacing is important and any kind of guideline is helpful. The golden ratio can work a bit like the rule of thirds: It can be a compositional convention or guide, but not a hard-and-fast regulation about how you should structure your work.
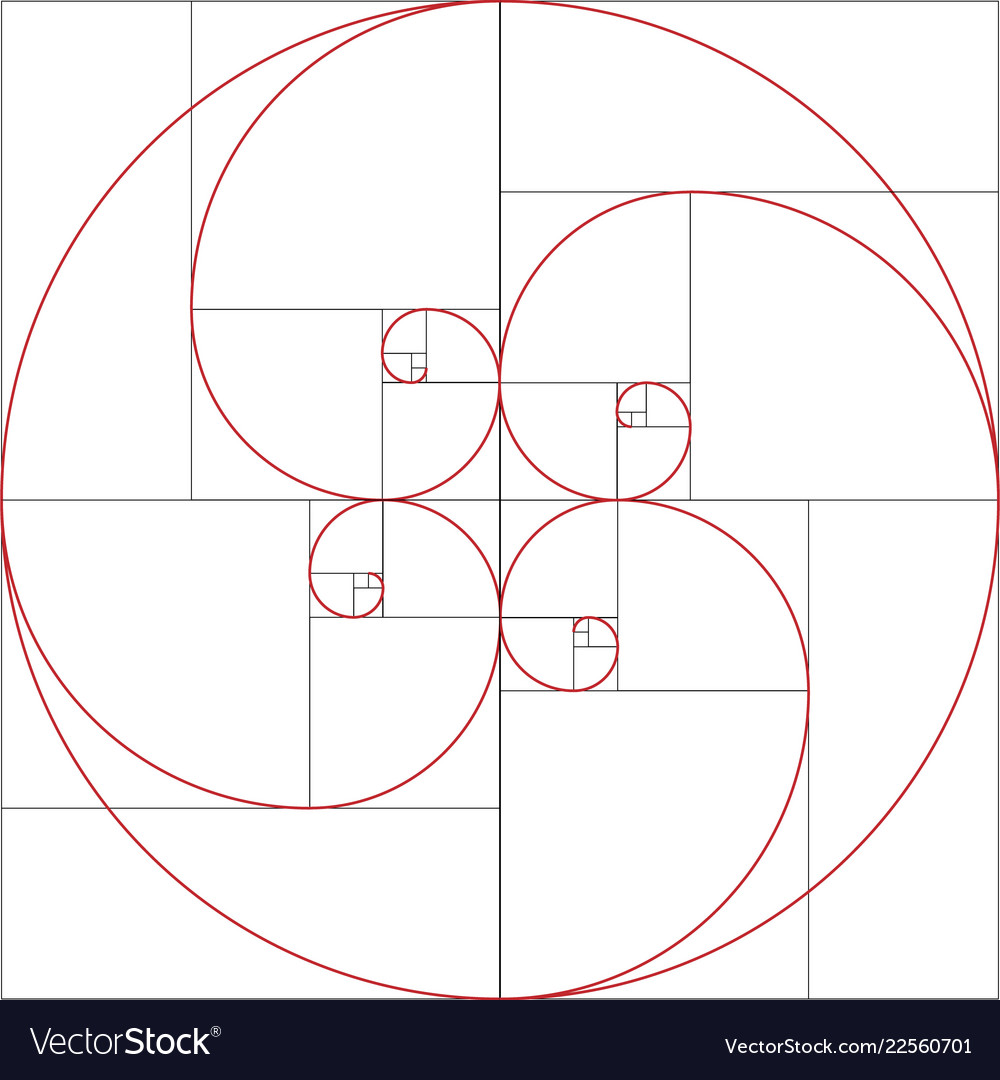
You can use the golden ratio to help guide you. The first few terms of the Fibonacci sequence are 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, and as the sequence progresses, the ratio of any term and its preceding term approaches the golden ratio. “On a graphic that might be pretty busy, so placement is everything,” says graphic designer Jacob Obermiller. Recall the the Fibonacci sequence is a sequence where the first two terms are 1 and then each subsequent term is the sum of the two previous terms. You can create a poor design that still conforms to the golden ratio, but you can use the golden ratio to inform your composition, to help you avoid clutter and create an orderly and balanced design. There’s no evidence that use of the golden ratio is better than use of other proportions, but artists and designers are always in the business of creating balance, order, and interesting composition for their work.Īesthetics and design don’t adhere to strict mathematical laws. Phi allows for efficient distribution or packing, so leaves that grow in relation to the golden ratio will not shade each other and will rest in relation to one another at what is known as the golden angle. Tree leaves and pine cone seeds tend to grow in patterns that approximate the golden ratio, and sunflower spirals and other seeds tend to hew close to phi. Binet’s Formula: The nth Fibonacci number is given by the following formula: fn (1 + 5 2)n (1 5 2)n 5. Phi does show up in other aspects of nature. As you find the ratio of successive numbers in the Fibonacci sequence and divide each by the one before it, you discover that the value gets closer and closer. It’s true that nautiluses maintain the same shell proportions throughout their life, but the ratio of their shells is usually a logarithmic spiral, as opposed to an expression of phi. Some seashells expand in proportion to the golden ratio, in a pattern known as a golden spiral, but not all shells do. The ratio of any two successive Fibonacci numbers is close to the Golden ratio, which is approximately equal to 1.618034. The proportions of nautilus shells and human bodies are examples of the golden ratio in nature, but these tend to vary greatly from one individual to the next. Golden ratio enthusiasts argue that the golden ratio is aesthetically pleasing because it’s common in the natural world.


 0 kommentar(er)
0 kommentar(er)
